Curso de Cálculo Numérico

Professor Raymundo de Oliveira

4-1 Métodos Diretos

Os Métodos Diretos triangularizam a matriz original dos coeficientes, permitindo, dessa forma, sua resolução.

Vamos admitir que temos que resolver um sistema triangular, isto é, um sistema onde na primeira equação podem aparecer todas as variáveis mas da segunda em diante já não aparece a primeira variável, da terceira em diante não aparece a segunda variável, da quarta em diante não aparece a terceira variável, etc., de modo que na última equação só aparece a última variável.

10 x₁ + 5 x₂ – 3 x₃ + 2 x₄ = 19

        6 x₂ – 4 x₃ + 2 x₄ =  0

               5 x₃ – 3 x₄ =  5

                     2 x₄ = 10

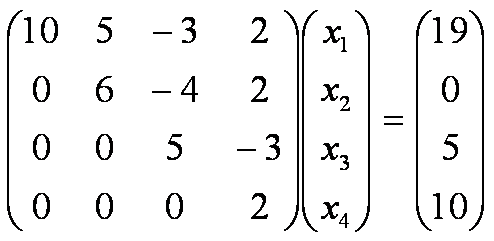
Como vemos trata-se de uma matriz triangular, onde abaixo da diagonal principal todos os elementos são zeros.

A resolução é muito fácil, calculando-se a partir da última variável para a primeira.

x₄ = 5              x₃ = 4              x₂ = 1              x₁ = 1,6

Se tivéssemos mil variáveis, a solução seria obtida, praticamente, com a mesma simplicidade, graças ao fato de o sistema ser triangular.

Vejamos dois Métodos Diretos:

4.1.1 – Métodos de Eliminação de Gauss

4.1.2 – Método LU


 

Se você tiver dúvidas sobre a matéria, meu e-mail é: raymundo.oliveira@terra.com.br