Curso de Cálculo Numérico

Professor Raymundo de Oliveira

4-1-2 Método LU

É muito comum ter-se que se resolver não um sistema A.x = B, e sim muitos sistemas onde só varia o lado direito B, mantida a matriz A. O método apresentado, Eliminação de Gauss, obrigaria a resolver tudo desde o início, para cada novo sistema. Um aperfeiçoamento desse método aproveita quase tudo o que já foi feito, permitindo que a solução de cada novo sistema, onde só variou o lado direito B, se dê rapidamente: é o método LU .

Dado um sistema A.X = B, pode-se fatorar a matriz A no produto de duas matrizes L e U, sendo L uma matriz triangular inferior e U uma matriz triangular superior.

Entende-se por matriz triangular inferior uma matriz que tem todos os elementos acima da diagonal principal iguais a zero.

Entende-se por matriz triangular superior uma matriz que tem todos os elementos abaixo da diagonal principal iguais a zero.

O método LU fatora a matriz A no produto L.U .

Há diferentes maneiras de se fazer essa fatoração; uma delas admite que os elementos da diagonal da matriz L são todos iguais a 1 , calculando-se a partir daí, todos os demais elementos de L e de U.

A matriz U resultante será a mesma matriz obtida quando se triangularizou a matriz A no método de Eliminação de Gauss.

Assim, quando se resolve um sistema  A X = B , é muito comum que não se trate simplesmente da resolução de um sistema e sim de diversos sistemas onde só se altera o vetor B, mantida a matriz original A.

Na verdade o vetor B, em geral, representa a condição de carga da estrutura, ou do circuito elétrico, ou das condições de contorno do problema a ser resolvido.

Durante o Método de Eliminação, para se eliminar a variável x_j da linha i usava-se a transformação L_i – a_ij / a_jj L_j ou L_i - m_ijL_j , onde m_ij = a_ij/a_jj .

Observe que m_ij é uma constante que multiplica a linha j para subtraí-la da linha i, eliminando dessa a variável x_j .

Chamemos de A⁽⁰⁾ a matriz original A do sistema A.X = B. Seja M (0) a matriz abaixo, formada pelos multiplicadores que eliminam a variável x₁ das linhas dois em diante.

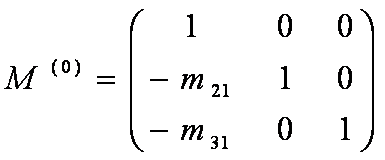
onde m₂₁ = a₂₁ / a₁₁   e   m₃₁ = a₃₁ / a₁₁ .

Ao multiplicarmos M ⁽⁰⁾ por A ⁽⁰⁾ obtemos A ⁽¹⁾, onde a variável x₁ já foi eliminada da segunda linha em diante.

Assim: M ⁽⁰⁾ . A ⁽⁰⁾ = A ⁽¹⁾

Seja M ⁽¹⁾ a matriz formada pelos  multiplicadores que eliminam a variável x₂ da terceira linha em diante.

onde m^* ₃₂ = a^* ₃₂ / a^* ₂₂ .

Ao multiplicarmos M ⁽¹⁾ por por A ⁽¹⁾ obtemos A ⁽²⁾ , onde a variável x₂ já foi eliminada da terceira linha em diante.

Assim: M ⁽¹⁾ . A ⁽¹⁾ = A ⁽²⁾

Admitindo-se um sistema de terceira ordem, três equações a três incógnitas, a matriz A ⁽²⁾ já estará triangularizada.

A ⁽²⁾ = M ⁽¹⁾.A ⁽¹⁾ = M ⁽¹⁾ . M ⁽⁰⁾ . A ⁽⁰⁾

Repetindo, onde A ⁽⁰⁾ é a matriz original e A ⁽²⁾ a matriz triangularizada.

A ⁽⁰⁾ = (M ⁽¹⁾.M ⁽⁰⁾)^-1 . A ⁽²⁾

porém, 

(M ⁽¹⁾.M ⁽⁰⁾)^-1 = (M⁽⁰⁾ )^-1.(M⁽¹⁾)^-1

Logo A⁽⁰⁾ =  (M⁽⁰⁾ )^-1. (M⁽¹⁾)^-1 . A⁽²⁾

Sendo

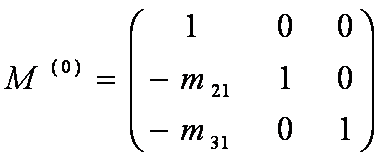
tem-se que

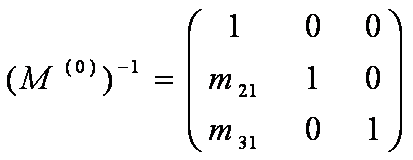
Isso pode ser verificado pois M⁽⁰⁾ . (M⁽⁰⁾ )^-1 = I , onde I é a matriz identidade.

Da mesma forma, sendo

O que pode ser verificado pois M⁽¹⁾ . (M⁽¹⁾ )^-1 = I , onde I é a matriz identidade.

Como    A⁽⁰⁾ =  (M⁽⁰⁾ )^-1. (M⁽¹⁾)^-1 . A⁽²⁾ , tem-se que a matriz original A⁽⁰⁾ vale:

Logo,

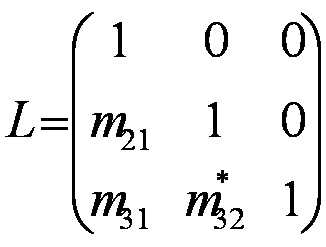
e U = A⁽²⁾ isto é, a matriz triangularizada.

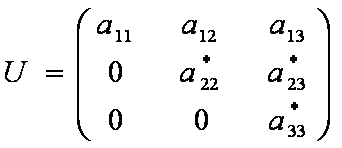
onde o * indica que a₂₂ , a₂₃ e a₃₃ não são os originais da matriz A.

Assim, conseguiu-se fator a matriz original A no produto de duas matrizes triangulares L e U , sendo L uma triangular inferior (lower) e U uma triangular superior (upper).

Repare que o fatorar A em L.U não dá mais trabalho que o método de Eliminação de Gauss em si, pois os multiplicadores m_ij são subproduto do próprio método.

A grande vantagem de se ter fatorado a matriz A é que, uma vez calculados L e U, pode-se resolver o sistema A . x = B transformando-se A em L.U e resolvendo-se dois sistemas triangulares, ou seja:

A . X = B \L . U . X = B ,

e fazendo-se U . X = Y , tem-se:

L . Y = B , sistema triangular de fácil solução, o que permite o cálculo imediato de Y.

Tendo-se Y e sabendo-se que U . X = Y , calcula-se X também com um sistema triangular, repito, de fácil e imediata solução.

Dessa forma, uma vez fatorado A em L . U , dado B calcula-se X pela resolução de dois sistemas triangulares, ou seja:

L . Y = B   e        U . X = Y .

No caso tão comum de se ter de calcular a solução de muitos sistemas A.X=B, uma vez fatorado A em L . U , basta tomar cada B e se calcular a solução resolvendo-se dois simples sistemas triangulares.

Havendo, portanto, vários sistemas a serem calculados para uma mesma matriz A e para diferentes B , o melhor caminho é fatorar A em L . U e resolver L . U . X = B.

Vejamos a solução do problema já dado anteriormente.

5,0 x₁ + 1,0 x₂ – 2,0 x₃ = 10

3,0 x₁ – 9,4 x₂ + 1,8 x₃ = 22

1,0 x₁ + 2,2 x₂ + 4,6 x₃ = 10

Inicialmente esquece-se do valor de B e trata-se de fatorar A.

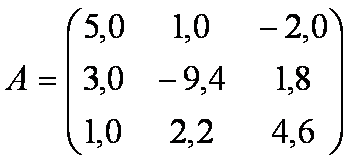
Usando-se o cálculo já feito para o método de Eliminação de Gauss, tem-se:

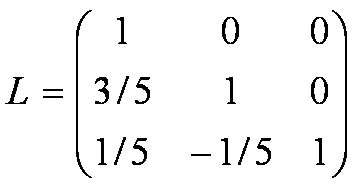
Se multiplicarmos L por U obteremos a matriz original A.

Para resolver o sistema A . X = B , dado um certo valor para o vetor B, segue-se o seguinte caminho:

A . X = B \L . U . X = B

fazendo-se U . X = Y , tem-se : L . Y = B

Logo:

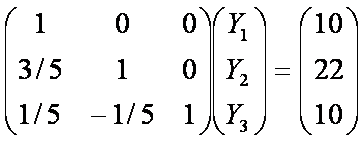
Logo: Y₁ = 10 , Y₂ = 16  e Y₃ = 11,2

Como U . X = Y , tem-se:

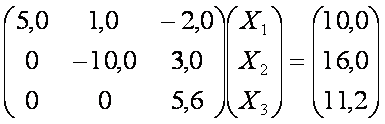
Daí, X₃ = 2,0  ,  X₂ = -1,0   e  X₁ = 3,0

Se mudássemos o valor do vetor B, tão comum nos problemas práticos, bastaria resolver os dois sistemas triangulares, pois a matriz A já está fatorada em L . U.

Se você tiver dúvidas sobre a matéria, meu e-mail é: raymundo.oliveira@terra.com.br