Curso de Cálculo Numérico
Professor Raymundo de Oliveira
Sistemas mal condicionados
Analisemos os dois seguintes sistemas de equações lineares.
5 x1 + 2 x2 = 10 5 x1 + 2 x2 = 10
10 x1 + 4 x2 = 20 10 x1 + 4 x2 = 30
Se traçarmos os gráficos dessas retas, veremos que no primeiro sistema as retas coincidem e no segundo são retas paralelas.
Assim o primeiro sistema terá infinitas soluções, pois todos os pontos das retas coincidentes atendem às duas equações.
Já no segundo sistema, caso em que as retas são paralelas, não haverá nenhum ponto capaz de atender às duas equações; as retas não se cortam.
Sistemas desse tipo são chamados sistemas singulares, podendo ser de solução indeterminada, quando há infinitas soluções ou de solução impossível, quando não há qualquer solução.
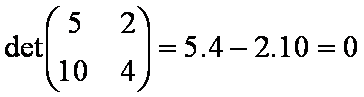
Em ambos os casos o determinante da matriz do sistema é nulo, como podemos verificar neste caso.
Em casos de sistemas de ordem mais elevada, não é óbvio, a um primeiro olhar, se o sistema é ou não singular.
Por exemplo, toda vez que uma linha ou uma coluna de uma matriz for uma combinação linear de outras linhas ou colunas, o determinante será zero. Imaginemos um sistema de 1000 equações a 1000 incógnitas, onde a linha 723 é igual à linha 234 x 1,9734 + a linha 532 x 3,9812 – a linha 159 x 0,9281.
Claro que nunca será perceptível essa relação, embora o determinante seja igual a zero e a solução, necessariamente será ou indeterminada ou impossível, com determinante do sistema igual a zero.
Imaginemos agora um outro caso, dado pelos sistemas abaixo.
5 x1 + 3 x2 = 15 5 x1 + 3 x2 = 15
5,01 x1 + 3 x2 = 15 5 x1 + 3,01 x2 = 15
O determinante do primeiro sistema vale 5 x 3 – 5,01 x 3 = - 0,03 e o determinante do segundo sistema vale 5 x 3,01 – 5 x 3 = 0,05, portanto ambos diferentes de zero.
Os dois sistemas tendo determinante diferente de zero, têm solução possível determinada, isto é, solução única.
No primeiro sistema a solução única é x1 = 0 e x2 = 5.
No segundo sistema a solução única é x1 = 3 e x2 = 0.
Reparem que os sistemas são praticamente iguais, podendo mesmo se considerar que as eventuais diferenças seriam devidas a erros de aproximação.
Entretanto, um pequeno erro está causando uma enorme diferença entre os resultados.
Sistemas como esses, tais que uma pequena diferença num coeficiente causa uma grande mudança nos resultados, são chamados Sistemas Mal Condicionados, em inglês “Ill Conditioned”.
O que caracteriza esses sistemas é que seu determinante é muito pequeno quando comparado a seus elementos. Verifique seus valores.
Sistemas como esses exigem grande cuidado, requerem que se trabalhe com a maior precisão possível, pois qualquer pequeno erro pode causar enorme variação nos resultados.
Voltemos ao sistemas singulares a que nos referimos há pouco. Imaginemos um sistema muito grande, em que uma das linhas seja combinação linear de outras linhas. Claro que o sistema será singular, com determinante igual a zero.
Na hora de resolver esse sistema, no processo de triangularização, deverá aparecer e não poderá ser retirado, um elemento da diagonal principal igual a zero, forçando seu determinante a ser zero.
Entretanto, com tantas contas, tantas aproximações, será que o cálculo do determinante dará mesmo zero ? É muito improvável ! Deve dar algo próximo a zero mas zero mesmo não creio.
Assim, um sistema singular tende a aparecer como um sistema mal condicionado, com determinante muito menor do que seria de se esperar.
É preciso estar atento a isso; um sistema mal condicionado pode ser originado por um sistema singular com erros devido às aproximações, aos truncamentos que necessariamente ocorrem nos cálculos.
Quando surgir um sistema mal condicionado, é possível, e mesmo provável, que haja algum erro na modelagem que deu origem ao sistema de equações lineares.
Se você tiver dúvidas sobre a matéria, meu e-mail
é: raymundo.oliveira@terra.com.br
![]()