
3.4 Método de Newton Raphson
Vimos no método de Iteração Linear que, dado f(x) = 0 , esta equação poderia ser transformada em x = g(x) e, daí, ser desenvolvido um processo iterativo onde, dado x0, seriam calculados x1= g(x0), x2= g(x1) ...xi+1= g( xi ), na expectativa de que a seqüência convirja para a raiz r.
Vimos, também, que há diferentes maneiras de se construir g(x), sendo que para alguns haverá convergência para a raiz e para outros não convergirá.
Além disso, a convergência dependerá do valor da derivada de g na região em torno da raiz, precisando ser, em módulo, menor que 1, para se ter convergência garantida para a raiz. Quanto mais próximo de zero, mais rápida será a convergência, pois cada novo erro será aproximadamente o valor do erro anterior multiplicado pela derivada de g na raiz.
A idéia central no método de Newton-Raphson é a de escolher uma função g, tal que a derivada de g, na raiz que se está procurando, seja 0(zero). Assim teremos, não só garantia da convergência quanto convergência muito rápida.
O método de Newton-Raphson é, também, conhecido como Método das Tangentes.
A idéia é a de se tomar um valor de x, isto é, da variável independente, como primeira estimativa da raiz. Com esse valor de x, calcula-se o valor da função que, provavelmente, não estará valendo zero, isto é, não se está na raiz. Desse ponto, traça-se a tangente à curva, buscando-se o ponto em que essa tangente corta o eixo de x. Esse novo valor de x deverá ser uma melhor aproximação da raiz.
A figura a seguir indica o processo a ser seguido.
Vamos admitir que se pretenda calcular a raiz de ex - 2 cos(x) = 0. Pelo gráfico vemos que a raiz está próxima a 0,5. Vamos tomar como primeira aproximação um valor mal escolhido, qual seja x0 = 1,0 . Calculamos f(x0 ) = f(1) = 1,6377 .
Traçamos pelo ponto (1,0 , 1,6377) uma tangente à curva e toma-se o ponto onde a tangente corta o eixo de X como a nova aproximação, x1 , da raiz.
Assim, x1 = 0,63 será a próxima aproximação, por onde será passada nova tangente, até se chegar a um valor que satisfaça quanto à precisão desejada. É bom observar que, aos poucos, havendo convergência, os valores começam a ficar muito próximos uns dos outros, praticamente se repetindo.

Veja que tg(a) = f '(x0) é igual a f( x0 ) / (x0 - x1 ) . Daí, supondo f '(x0) diferente de zero, tem-se que:
x0 - x1 = f( x0 ) / f '(x0) . Assim, a nova estimativa x1 = x0 - f( x0 ) / f '( x0)
Assim, para se calcular a raiz de f(x) = 0, a função g de iteração, escolhida, é a seguinte: x = g(x) = x - f(x)/f '(x) , onde se precisa garantir que f ' seja diferente de zero.
Vamos calcular g ' (r).
g '(x) = 1 - ( f ' . f ' - f . f '' )/ (f ')2 = f . f '' / (f ')2 .
Sendo f(r) = 0 , por definição, por se estar exatamente procurando a raiz r de f , e sendo f ' diferente de zero, tem-se que g ' (r) = 0. Dessa forma, sendo f ' diferente de zero, tem-se convergência garantida e rápida.
Exemplo: calcular a raiz positiva de ex - 2 cos(x) = 0
x = g(x) = x - (ex - 2 cos(x) / (ex + 2 sen(x)
Pelo gráfico abaixo, vê-se que a raiz está próxima a 0,5
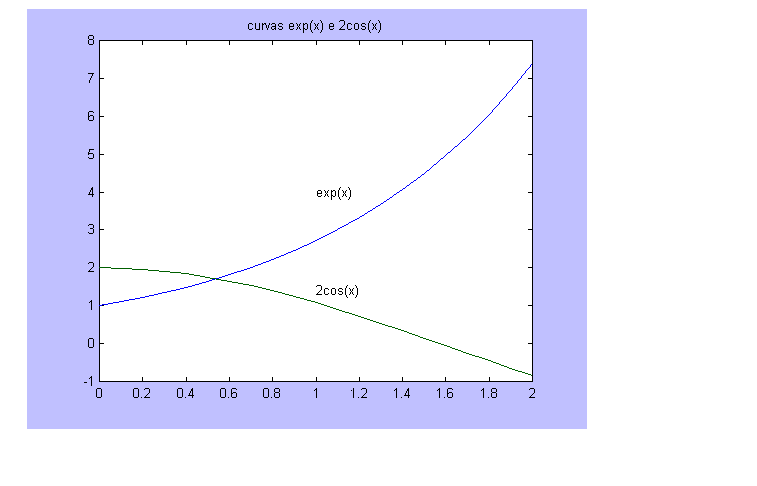
Partindo de x0 = 0,5 , calcula-se:
x1 = g(x0) = x0 - (exp( x0 )- 2 cos(x0) / (exp( x0 ) + 2 sen(x0)
x1 = 0,540821
x2 = g(x1) = x1 - (exp( x1 ) - 2 cos(x1) / ( exp( x1 ) + 2 sen(x1)
x2 = 0,539786
x3 = 0,539785
x4 = 0,539785
Como se vê, chega-se rapidamente à raiz com seis decimais.
No método de Newton-Raphson, a convergência não é linear, como no Método da Iteração Linear. A convergência é mais rápida, é quadrática. Assim, cada novo erro é proporcional ao quadrado do erro anterior.
Vejamos por que.
Pelo desenvolvimento em Série de Taylor, sabe-se que:
g(r+e) = g(r) + g'(r).e /2! + g''(r).e2 / 2! + g'''(r). e3 / 3! + ...
Como se fez a transformação de f(x) = 0 para x = g(x) , onde g(r) = r e xi+1 = g( xi ) , tem-se:
xi = r + ei , onde ei é o erro que se comete se considerarmos que xi = r
xi+1 = r + ei+1 , onde ei+1 é o erro que se comete se considerarmos que xi+1 = r
Temos que xi+1 = g( xi ) , onde xi = r + ei
Assim, g( xi ) = g(r + ei ) = g(r) + g'(r).ei + g''(r).ei2 / 2! + g'''(r). ei3 / 3! + ...
Sendo f '(x) diferente de zero, vimos que g'(r) = 0 .
Vamos admitir que estamos com erro pequeno, de forma que e3 possa ser desprezado em face de e2
Daí, g( xi ) = g(r + ei ) ~ g(r) + g''(r).ei2 / 2!
Lembrando que g(r) = r e xi+1 = g( xi )
xi+1 = r + g''(r).ei2 / 2!= r + ei+1
Logo: ei+1 = (g''(r)/ 2).ei2 = K . ei2 , com convergência quadrática.
Teste seus conhecimentos, procurando calcular as raízes abaixo, estimando, primeiro um valor inicial pelo método gráfico.
1 - f(x) = e2x - 3 cos(x) = 0 .... Calcular a raiz positiva e a maior raiz negativa.
2 - f(x) = ex + x -2 = 0
3 - f(x) = e-x - sen(x) = 0 ...Calcular as três menores raízes positivas.
4 - f(x) = ex . sen(x) - cos(x) = 0 ... Calcular as duas menores raízes positivas.
Não é difícil demonstrar que, no caso de raiz dupla, quando se tem f(x) = 0 e f '(x) = 0 , a convergência é linear e não quadrática.
Vimos acima que g '(x) = f . f '' / (f ')2 e daqui só pudemos afirmar que g '(r) = 0 pois f(r) = 0 se f '(r) fosse diferente de zero. No caso de raiz dupla tem-se f '(r) = 0 e, portanto, g '(r) = 0 / 0 , indeterminado.
Para levantar esta indeterminação aplicamos a Regra de L' Hospital, derivando o numerador e o denominador.
g '(r) = (f . f ''' + f ' . f '') / 2 f '.f '' = 0 / 0 . Derivando, mais uma vez, o numerador e o denominador, tem-se:
g '(r) = ( f . f'''' + f '.f''' + f ' . f ''' + f '' . f '') / (2(f '.f ''' + f '' . f '' ) = 1/2
Como ei+1 ~ g'(r).ei , tem-se convergência linear, com razão de convergência igual a meio, isto é, cada novo erro é aproximadamente igual à metade do erro anterior.