Método da Iteração Linear

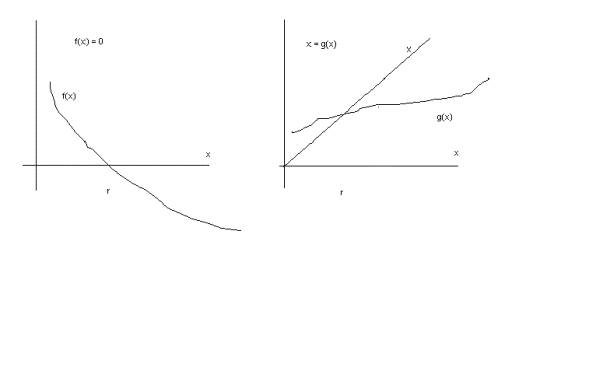
Quando se busca a raiz de f(x) = 0, está-se procurando o ponto em que a função f(x) corta o eixo x. O Método da Iteração Linear (MIL) transforma o problema, procurando isolar o x da função f, de modo a se ter x = g(x). A partir desse ponto, busca-se a interseção da reta x com a curva g(x).

Dessa forma, o método transforma o problema de se encontrar uma raiz da equação f(x) = 0 na busca de se encontrar o ponto em que x = g(x).

Seja a equação f(x) = e^x + x – 2 = 0 . Podemos isolar x , de f(x), de diferentes maneiras:

x = 2 – e^x = g₁(x)

e^x = 2 – x , donde, x = ln(2 – x) = g₂(x)

ou, somando x aos dois lados de f(x) = 0

x = e^x + 2x – 2 = g₃(x) etc...

O fundamental é que resolvendo-se o problema x = g(x) , ter-se-á resolvido o problema f(x) = 0 .

Os dois gráficos abaixo mostram a transformação de um problema no outro.

Vejamos o que acontece numa equação do segundo grau:

f(x) = x² – 5x + 6 = 0 .

Sabemos que 3 é raiz , pois f(3) = 3² – 5. 3 + 6 = 0 .

Isolando-se x temos: x = (x² + 6)/5 = g(x) .

g(3) = (3² + 6)/5 = 3 . Assim, se f(3) = 0, tem-se que g(3) = 3.

Dessa forma se resolvermos x = g(x) , teremos resolvido f(x) = 0.

A vantagem que se obtém, em alguns casos, é que se pode transformar a resolução do problema num processo iterativo, a partir de uma aproximação inicial que se tenha da raiz.

Vamos supor que se sabe que a raiz está próxima a um valor x₀ . Calcula-se g(x₀). Se g(x₀ ) = x₀ , ter-se-á chegado à raiz.

O provável é que isso não ocorra e que g(x₀) ¹ x₀ . Nesse caso, g(x₀) = x₁ passa a ser o próximo valor a ser testado como raiz. O processo se repete fazendo-se x_i+1 = g(x_i).

Em determinadas condições, a seqüência x₀ , x₁ , x₂ ... converge para a raiz r.

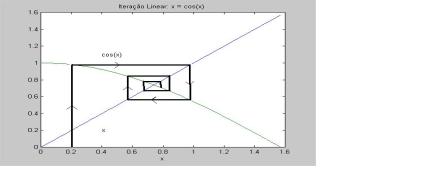
O gráfico a seguir ilustra esse processo.

Vejamos um exemplo numérico. Calcular a raiz de f(x) = e^x + x –2 = 0

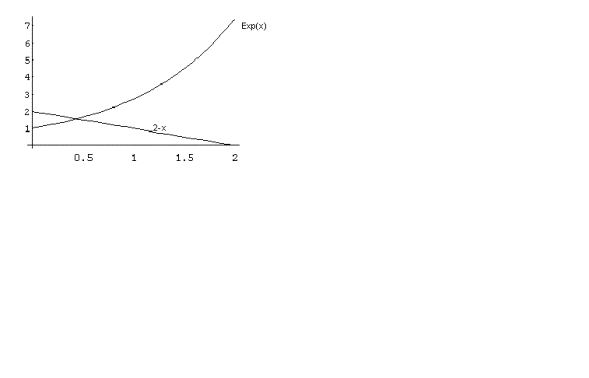
Fazendo a transformação e^x = 2 – x , e fazendo os gráficos dessas duas funções,

Vemos que a raiz está próxima a 0,5. Vamos tomar, portanto, 0,5 como nossa hipótese inicial para a raiz r.

x₀ = 0,5

Vamos transformar f(x) = 0 em x = g(x) . Isso pode ser feito de diferentes maneiras:

a) x = ln(2-x) = g₁(x)

b) x = 2 – e^x = g₂(x)

c) x = e^x + 2x – 2 = g₃(x)

d) ....

Tomemos a primeira maneira: a) x = ln(2-x) = g₁(x)

Calculemos g₁(0,5) = ln(2 – 0,5) = ln(1,5) = 0.405465 ¹ 0,5

A nova aproximação para a raiz será x₁ = 0.405465

g₁(x₁) = ln(2-0.405465) = ln(1,594535) = 0.466582 = x₂

g₁(x₂) = ln(2-0,466582) = ln((1,533418) = 0.427499 = x₃

g₁(x₃) = 0.452667

g₁(x₄) = 0.436533

g₁(x₅) = 0.446906

g₁(x₆) = 0.440313

g₁(x₇) = 0.444485

...

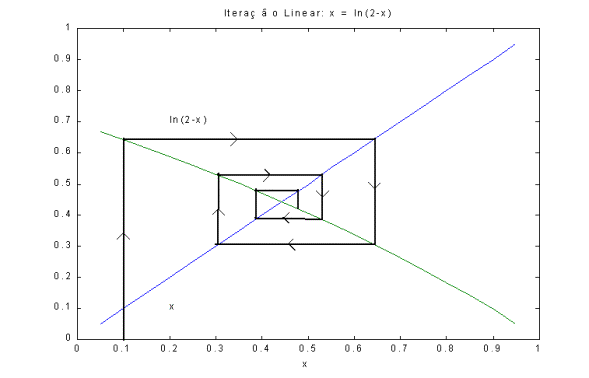
A raiz converge para aproximadamente r = 0,44

O gráfico abaixo mostra a convergência, passo a passo.

Tomemos, agora, a segunda maneira indicada acima, de se obter g(x).

b) x = 2 – e^x = g₂(x)

Partindo de 0,5 , nossa primeira estimativa, vamos procurar melhorá-la, a exemplo do que foi feito com g₁(x).

g₂(0,5) = 2 – e^0,5 = 0.351279

g₂(0.351279) = 0.579117

g₂(0.579117) = 0.215539

g₂(0.215539) = 0.75947

g₂(0.75947) = -0.137144

g₂(-0.137144) = 1.12816

.....

Não está convergindo para a raiz 0,44 , e, sim, se afastando dela, ora pela direita, ora pela esquerda.

Logo o método nem sempre converge !

O gráfico abaixo mostra o que aconteceu.

(gráfico 3)

Esquematicamente, há quatro possibilidades, quando se busca a interseção de x com g(x), o que é mostrado abaixo.

(figura 4)

Nos gráficos a e c há convergência, nos b e d não há convergência.

Observemos que em a , a derivada de g é positiva e menor que 1; em b a derivada é positiva e maior que 1; em c a derivada é negativa e maior que –1 e , finalmente, em d a derivada é negativa e menor que –1.

Dessa forma, vemos graficamente, que há convergência quando a derivada de g está entre –1 e +1.

Vejamos, analiticamente, porque isso acontece.

Antes de mais nada, vamos recordar um dos muitos teoremas do Valor Médio, estudado nos cursos de Cálculo.

Seja g(x) uma função contínua e diferenciável num intervalo (a,b). Haverá sempre, pelo menos um ponto c Î (a,b) , tal que g^’(c) = (g(b) – g(a))/(b-a) .

Graficamente, a informação implica em que há pelo menos um ponto c pertencente ao intervalo aberto (a,b) , tal que a tangente em c é paralela à secante que passa pelos pontos a , g(a) e b , g(b).

A figura abaixo ilustra a informação, mostrando que pode haver mais de um ponto c.

(figura 5)

Observa-se que: tg(a) = g’(c) e que tg(a) = (g(b) – g(a))/ (b-a).

Voltando à função x = g(x), onde x₀ é a aproximação inicial da raiz r, onde g(r) = r.

Tem-se a seqüência:

x₁ = g(x₀)

x₂ = g(x₁)

x₃ = g(x₂)

...............

x_i+1 = g(x_i)

...............

r = g(r)

Logo, x_i+1 – r = g(x_i) – g(r)

Pelo Teorema do Valor Médio, visto acima, g(x_i) – g(r) = g^’(x_i)(x_i – r),

onde x_i Î (x_i , r) .

Daí: x_i+1 – r = g^’(x_i)(x_i – r) . Donde: ½x_i+1 – r ½= ½g^’(x_i) ½.½ x_i – r ½

Porém, ½x_i+1 – r ½ é o módulo do erro depois de i+1 iterações (e_i+1) e ½ x_i – r ½ é o módulo do erro depois de i iterações (e_i) .

Assim, ½e_i+1½ = ½ g^’(x_i) ½.½e_i ½. Dessa forma, o novo erro será menor que o erro anterior se ½ g^’(x_i) ½< 1. A partir daí, pode-se demonstrar que sendo ½ g^’(x_i) ½< 1 o erro e_i tende a zero se i tende a infinito. (bibliografia 3 pag. ...). Sendo e_i = x_i – r , temos que x_i tende a r.

A condição é suficiente mas não necessária. É suficiente, isto é, havendo um intervalo I = (r-d, r+d) onde ½ g^’(x) ½< 1 , para todo x Î I , então, para qualquer x₀ Î I , a seqüência x₀ , x₁ , x₂ , .... , x_i tende a r, se i tende a infinito. Mas, não é necessária, pois pode haver um intervalo onde nem sempre ½ g^’(x) ½ seja menor que 1 e ainda assim haja convergência, como indica a figura abaixo.

Vejamos o que ocorreu nos dois exemplos apresentamos acima.

No primeiro, onde houve convergência, foi feita a transformação x = ln(2-x) = g₁(x). A derivada g^’₁(x) = -1/(2-x). Sendo a raiz próxima a 0,5 temos: g^’₁(0,5) = -1/1,5 = -0,67. Assim, |g^’₁(0,5)| < 1. Haverá, necessariamente, convergência para a raiz.

No segundo exemplo, onde não houve convergência, tinha sido feita a transformação x = 2 – e^x = g₂(x). A derivada g’₂(x) = – e^x . Sendo a raiz próxima a 0,5 , tem-se: g’₂(0,5) = -e^0,5 = -1,65. Assim, |g’₂(0,5)| > 1, o que não garante convergência. No caso não houve, como se viu, convergência.